dh/dt = v
dv/dt = -g + bv2
Here g and b are constants. What is the terminal velocity of the parachute? Write down a numerical scheme for solving these equations using Euler's method.
Ans:
dh/dt = v dv/dt = -g + bv2Terminal Velocity is reached when dv/dt = 0 i.e. velocity no longer increases, and the velocity settles to a large fixed value.
dv/dt = 0 -g + bv2 = 0 v2 = g/b v = +/- (g/b)0.5 therefore, terminal velocity = -(g/b)0.5Euler's Method:
vn+1 = vn + an dt xn+1 = xn + vn dt where a = F(x,v)/m therefore: vn+1 = vn + (-g + bvn2)dt hn+1 = hn + vn dt
Ans:
Fractals are rough or fragmented geometric shapes which can be sub-divided into parts, each of which is at least approximately a reduced size copy of the whole.
Simple geometric objects are those with regular or ordered shapes.
An example algorithm for generating fractals:
Iterated Function Systems: x -> Mx + c where M is a NxN matrix c is a N-component column vector
Ans:
Advantages:
Introduction of grids with large spacing saves CPU time and memory
requirements, which is particularly important for solving large systems.
Disadvantages:
Details of weather patterns cannot be described. Anything between
2 grid points is lost.
Long term weather forecasting is difficult because the memory and
CPU time requirement is beyond the capability of current computer systems.
Ans:
For each particle in the system, Newton's 2nd Law is applied in each dimension:
Fx = max = m d2x/dt2 Fy = may = m d2y/dt2 Fz = maz = m d2z/dt2 where x, y, z denote the position of the particle; vx, vy, vz denote the velocity of the particle ( vx = dx/dt, etc... ) ax, ay, az denote the acceleration of the particle ( ax = dvx/dt = d2x/dt2, etc... )Therefore 3 coupled ODEs are needed for each particle. For N particles, the total number of ODEs is 3N.
The initial conditions required:
- Starting position of each particle (x0, y0, z0)
-
Starting velocity of each particle (Vx0, Vy0,
Vz0)
Ans:
We model the system Using the simple population growth model:
Nuclei A population: NA
Nuclei B population: NB
Population change (rate): dNA/dt and dNB/dt
Relationship:
- A decays to B:
k A -----> B NA decreases by kNA NB increases by kNA
k B -----> A NB decreases by kNB NA increases by kNBRate Equations:
dNA/dt = -kNA + kNB dNB/dt = -kNB + kNAA and B react to give rise to C, so:
NA decreases by kNANB NB decreases by kNANB NC increases by kNANBTherefore, Rate Equations:
dNA/dt = -kNA + kNB -kNANB dNB/dt = -kNB + kNA -kNANB dNC/dt = kNANB
Wireframe, ball-and-stick, spacefill.
To view: Use Chemistry => View Molecule in Rasmol to view the
molecule in 3D.
To save: Use File => Import => Molfile
(1) 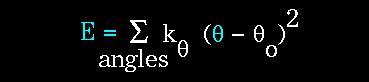
(4) and (2) 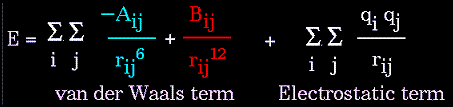
(3) 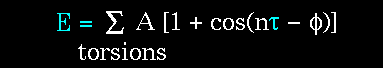
- Brookhaven protein databank: 3D crystal and NMR structure
- SWISS-PROT:Annotated protein sequence database.
- SCOP: Structural classification of proteins.
- The national center for biotechnology information: Integrated ENTREZ retrieval software, BLAST search tools and databases for genetics, gene and protein sequences, 3D structures, and on-line PubMed library.
-
The genome database: Datebase for genes of human and other species.
of proteins, DNA, RNA and ligand-bound complexes.
Ligand-protein docking